Enhancing Qubit Control: The Power of Phase-Modulated Pulses

Imagine you’re trying to tune an old-school radio to your favorite station. You carefully turn the dial, but the signal keeps drifting, and static hisses fill the gaps in your favorite song. Now, picture trying to control quantum bits, or qubits, with similar precision, but instead of just static, even the tiniest error can throw off complex quantum computations. Just like finding that perfect frequency on the radio, researchers are continuously seeking ways to achieve high-fidelity control over qubits.
Recently, researchers from Aalto University [1] have made a breakthrough in this field, developing a method for robust qubit control using phase-modulated pulses. Their approach promises to enhance the reliability of quantum operations, moving us closer to practical quantum computing. Interestingly, they discovered this technique somewhat serendipitously while investigating various machine learning techniques for qubit control. The researchers found that phase modulation provided a much simpler and neater solution compared to more complex methods. So, let’s have a closer look at this elegant approach:
The Quest for Quantum Control
Quantum control involves the precise manipulation of qubits to perform specific operations, which is fundamental to the functioning of quantum computers. Traditional methods often rely on shaping the envelope of control pulses, which can be highly sensitive to errors in amplitude and frequency, leading to decreased fidelity of quantum operations. Addressing these challenges, Gheorghe Sorin Paraoanu’s research group at Aalto University has introduced a novel method of utilizing phase-modulated pulses.
This approach focuses on modulating the phase of the control field, significantly improving robustness against variations in drive amplitude of up to 20% and detuning up to tens of MHz. These enhancements ensure high-fidelity qubit operations even under non-ideal conditions.
Experimental Setup and Validation
To validate their approach, the researchers conducted experiments using Transmon qubits, a popular choice in superconducting quantum computing due to their relatively long coherence times and established fabrication techniques. The phase-modulated pulses were generated by utilizing Quantum Machines OPX+ system, in which intermediate-frequency signals were mixed with the local oscillator to produce the desired phase-modulated pulses.
For the measurements, the Transmon qubits were initialized in their ground state. The researchers employed a dispersive readout method using a highly detuned superconducting resonator coupled to the qubit, which allowed for precise measurement of the qubit states. The qubits used in the experiment had a relaxation time T1 ≈ 7μs and a coherence time T2 ≈ 5μs, ensuring sufficient time to perform the necessary operations and measurements.
Methods and Experimental Procedure
The experiment primarily focused on two fundamental operations: transferring qubits from the ground state to the excited state and performing arbitrary X/Y rotations on the Bloch sphere.
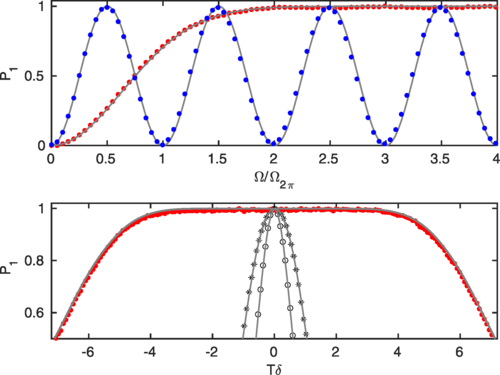
For these purposes, chirped pulses were used for the state transfer operation, which involved sweeping the frequency of the pulse during its application. This technique is particularly effective for achieving high-fidelity transfers between different states, even in the presence of frequency errors: the chirp ensures that the resonance condition is met at some point during the drive. Technically, this was achieved by modulating the phase of the control field in a linear fashion. Along with the smooth super-Gaussian envelope this, by design, counteracts deviations in both the drive amplitude and frequency detuning, as shown in Figure 1.
For implementing arbitrary rotations on the Bloch sphere, the researchers used phase-modulated pulses designed to drive the qubit along precise trajectories. The modulation patterns were tailored to perform rotations around the X and Y axes with high accuracy. The sequences of phase-modulated pulses were then tested for their ability to achieve the desired rotations, with fidelity measurements indicating robust performance even in the presence of control errors. Most remarkably, they achieved a population transfer with a fidelity greater than 99.9%, while maintaining robustness against detuning up to ±40 MHz.
Figure 1: (Top) Shows how well the super-Gaussian pulse (red dots) maintains its performance across different amplitudes compared to a standard non-modulated Rabi pulse (blue dots). (Bottom) Illustrates the stability of the super-Gaussian pulse (red dots) against frequency detuning, with the experimental data (red dots) closely matching the theoretical predictions (solid gray lines). Gray circles and stars represent the performance of standard Rabi pulses under similar conditions. Source: [1] Kuzmanović, Marko, et al. “High-fidelity robust qubit control by phase-modulated pulses.” Physical Review Research 6.1 (2024): 013188, reported here under Creative Common 4.0 license.
Phase modulation with OPX+: a simple code for a complex task
For their experiments, using the OPX+ and QUA, Quantum Machines’ intuitive programming language, made it incredibly easy for the researchers to program and execute their technique – as phase modulation can be directly encoded in the “I” and “Q” quadratures of the pulse to be played!
The code snippet below demonstrates how easily the robust population transfer operation can be implemented (a huge thanks to Dr. Marko Kuzmanović for providing the code!). You can also find the code on our GitHub Repository [2] and apply the technique to your own qubits!
First, we begin by defining the pulses:
def supergaussian(length, order, cutoff): x = np.linspace(-1, 1, length) return np.exp(x ** order * np.log(cutoff))def robust_wf(amp,length,mod=40e6,order=4,cutoff=1e-2): robust_time = np.linspace(-length / 2, length / 2, length) * 1e-9 robust_freq = np.linspace(-1, 1, length) * mod robust_envelope = supergaussian(length, order, cutoff) robust_rescaling = length / robust_envelope.sum() return robust_amp * robust_rescaling * robust_envelope * np.exp(1j * 2 * np.pi * robust_time * robust_freq)# Parameters for the robust waveform robust_len=200 robust_amp=0.1 # Select the type of pulse to generate using the match-case structure # pulse_flag = 2 # 0 for rectangular, 1 for super-Gaussian, 2 for robust pulse # Generate the pulse based on the selected flag match pulse_flag: case 0: pulse = robust_wf(robust_amp,robust_len,mod=0,order=4,cutoff=1) # rectangular pulse case 1: pulse = robust_wf(robust_amp,robust_len,mod=0,order=4,cutoff=1e-2) # super-Gaussian pulse case 2: pulse = robust_wf(robust_amp,robust_len,mod=40e6,order=4,cutoff=1e-2) # robust pulse # Update the pulse waveforms in the co: I = real(pulse) and Q=imag(pulse)!!! config['elements']['qubit']['operations'].update({'pulse':'robust_pulse'}) config['pulses'].update({"robust_pulse": {"operation": "control","length": robust_len,"waveforms": {"I":"I_wf","Q":"Q_wf",},}}) config['waveforms'].update({"I_wf": {"type": "arbitrary", "samples": np.real(pulse).tolist()}}) config['waveforms'].update({"Q_wf": {"type": "arbitrary", "samples": np.imag(pulse).tolist()}}) # Plot the real and imaginary parts of the generated pulse plt.plot(np.real(pulse)) plt.plot(np.imag(pulse))
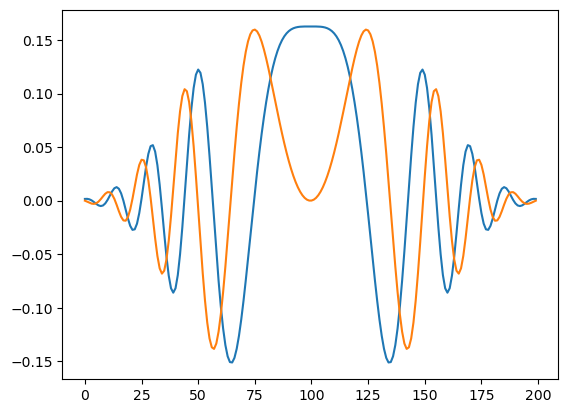
We can visualize the pulse generated by the code shown in Figure 2:
Figure 2: Visualization of the robust, phase modulated pulse with super-gaussian envelope. Courtesy of Dr. Marko Kuzmanović from the Paraoanu Team in Aalto University.
Finally, a straightforward QUA program implements a Rabi chevron experiment, allowing us to test how these pulses perform in the presence of amplitude and frequency errors:
with program() as rabi_amp_freq:
with for_(n, 0, n < n_avg, n + 1):
with for_each_(a, a_array.tolist()):
with for_each_(detuning, detuning_array.tolist()):
update_frequency('qubit', detuning + qubit_IF)
play('pulse' * amp(a), 'qubit')
align('qubit', 'resonator')
measure_dual_demod()
Executing the QUA program on a transmon qubit, then yields the following results:
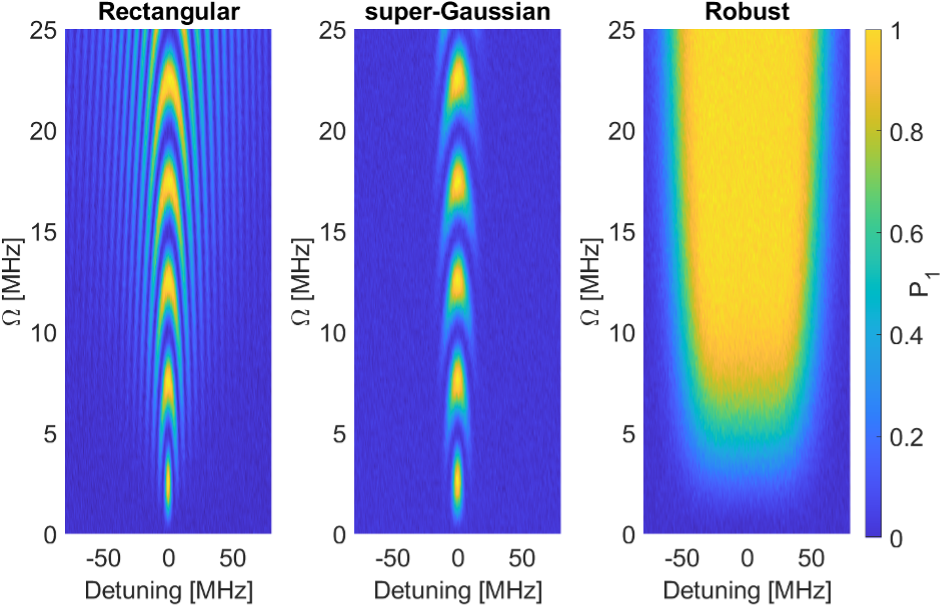
Figure 3: 2D Rabi Chevron plots comparing the robustness of different pulse shapes (Rectangular, Super-Gaussian, and phase modulated super-Gaussian ) against detuning (horizontal axis) and amplitude (vertical axis). These plots expand on the insights from Fig. 1 by showing a more comprehensive 2D sweep of the qubit’s response. Compared to the non-modulated pulses, the flat plateau with P1~1, visible on the third subplot, showcases the robustness of the modulated pulse to amplitude and frequency errors. Source: Dr. Marko Kuzmanović from the Paraoanu Team in Aalto University.
In this case using a rectangular pulse shows high sensitivity to detuning and amplitude variations with narrow bands of optimal performance. Using a super-Gaussian envelope reduces the pulse bandwidth, and at the same time increases the sensitivity to frequency errors. Utilizing the phase modulated pulse with a super-Gaussian envelope demonstrates the highest resilience, maintaining high fidelity across wide detuning and amplitude variations.
Key Benefits of Phase-Modulated Pulses
Compared to traditional control methods, phase-modulated pulses offer significant advantages: They require minimal to no optimization parameters, and provide better resilience against parameter drifts and fluctuations, while being as easy to implement. Additionally, this technique is hardware-agnostic, making it applicable across various quantum computing platforms.
At Quantum Machines, we are proud to support the novel research at Aalto University and eagerly anticipate their next developments in quantum control techniques. The application of phase-modulated pulses, combined with real-time qubit frequency updates as demonstrated in the Rabi experiment above, marks a significant advancement in achieving high-fidelity quantum operations. These improvements are vital contributions to the ongoing efforts toward developing practical and scalable quantum computers.
Discover More About Phase-Modulated Pulses for Qubit control
Are you intrigued by the potential of phase-modulated pulses to revolutionize qubit control? Join us for an upcoming online seminar where we’ll dive deeper into this groundbreaking research. You’ll have the opportunity to hear directly from the experts behind these innovations and explore how these techniques can enhance your quantum computing projects.
Don’t miss this chance to learn more and ask your questions during the live session!
Register to the online seminar here.
You can also explore the details further by checking out the research paper on Physical Review Research [1] and check out the code on Github [2].
Contact us or request a demo to learn more about OPX+ and its scaled-up version OPX1000 to better understand how these unique processor-based controllers can accelerate your research.
References
[2] Quantum Machines’ github repository: robust qubit control by implementing phase-modulated pulses.