Quantum Control for Semiconductor Spin Qubits

Control suite for spin qubits

Semiconductor quantum dot spin qubits are based on electrons or holes, electrostatically trapped and cooled down to millikelvin temperatures. Their spins are used for quantum information encoding and they are one of the leading technologies on the path to useful quantum computers. Trapping can be done in several ways, and while here we focus on electrostatic trapping (achieved using gate electrodes), most of the physics remains the same for other types of quantum dots such as donor and physically defined quantum dots.

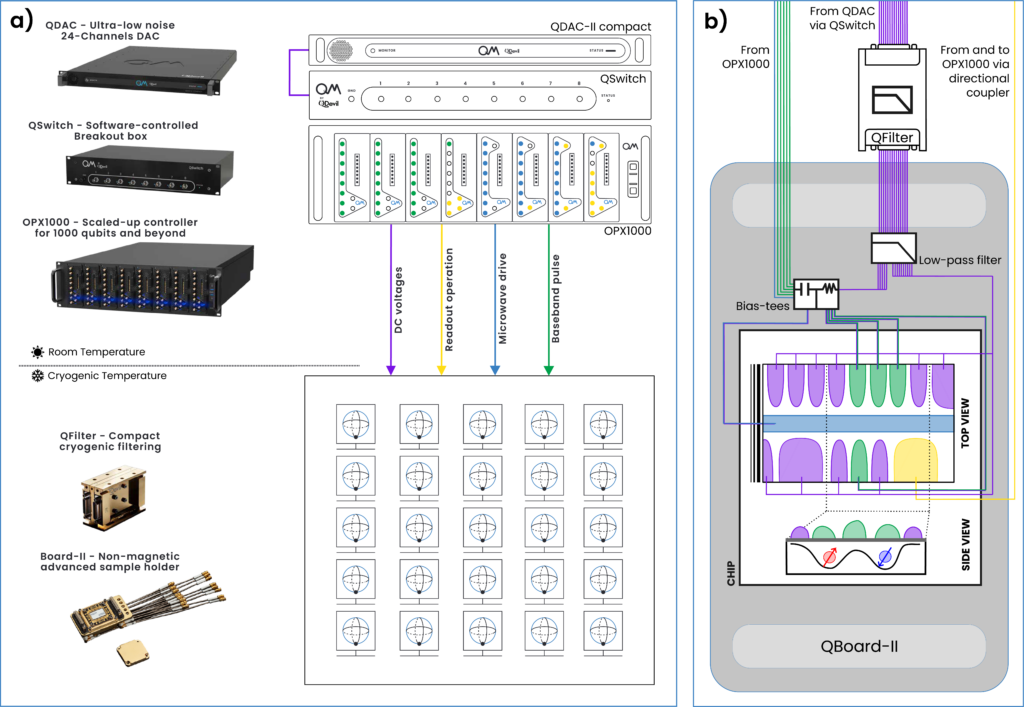
Figure 1: (a) Quantum Machines’ suite to control spin qubit devices. (b) Zoom-in on the chip carrier showing example connections for a two-qubit system.

By using electrostatic electrodes, the electron occupancy can be controlled down to a single electron, meaning we can decide to have zero, one or more electrons in the confining potential defining the dot. Such quantum dots can be positioned next to one another, creating an array or a network. Subsequently, by applying a magnetic field, the degeneracy of the spin state of the single electrons are lifted and can now be used to encode quantum information. Single qubit gates can be executed by precise control pulses applied to the electrostatic potential, while two-qubit gates are usually done via electron wavefunction overlaps with fast control pulses on the electrodes.

As of today, multiple material platforms and different qubit realizations with different quantum information encoding schemes are being pursued, and each of them has different control requirements. However, all these platforms share one fundamental need: they require low noise, ultra-stable radiofrequency (RF), microwave frequency (MW) and baseband pulses. Quantum Machines’ product portfolio enables the full control of spin qubits, ranging from room temperature to cryogenic electronics. Figure 1 shows a diagram with a typical setup for a spin qubit experiment powered by Quantum Machines’ control suite.

While the QDAC-II compact (as well as the QDAC-II) offers 24 stable and low-noise channels to power up the electrodes, Quantum Machines’ programmable switch matrix unit QSwitch, automates measurements of multiple spin qubits.

OPX1000 with its low frequency front-end module (LF-FEM) and microwave module (MW-FEM) is the ideal tool for performing readout, single- and two-qubit gates and executing advanced quantum algorithms. The OPX suite (OPX1000 and OPX+ for small-scale quantum devices) covers all the needs of the spin qubit community and continuous improvement allows it to be a flagship product in the field. The combination of the two FEMs offers the generation of signals from DC to 750 MHz (LF-FEM) and from 50 MHz to 10.5 GHz based on Digital Direct Synthesis (MW-FEM), at a sampling rate of 2 GSPS, voltage swing of 5 Vpp and record-low phase and voltage noise performance. Qubit drive, readout, computation and processing all happen in the same control platform – which is responsible for orchestrating the entire quantum circuit or experiment. It’s all written in the easiest possible way thanks to QUA, OPX’s powerful pulse-level language.

Spin qubits require very low temperatures, achieved by placing quantum dot devices inside a dilution refrigerator. To ensure cold electrons, it is important to take care of filtering the control lines that are coupled to them. To this end, Quantum Machines offers the combination of QFilter and QBoard-II which have been proven to allow for electron temperatures as low as 22 mK, measured on single electron transistors and Coulomb blockaded devices [1–2].  

All in all, Quantum Machines control suite is a complete control solution for any spin qubit experiment, going from simple setups all the way to the highest of scales, pushing for fault tolerant useful machines. 

Initializing a semiconductor device

Once the spin qubit network is cold inside the dilution refrigerator, the first step is to characterize the basic properties of the device, such as gate electrodes status. This can be easily done using Quantum Machines’ QDAC-II, which enables leakage matrix capabilities. QDAC-II and QDAC-II Compact are 24-channel DACs offering ultra-low noise (< 8 nV/√Hz) and high accuracy voltages with 25-bit resolution over a +/- 10V and +/- 2V. Users can independently configure each channel’s output filters, voltage, voltage range, current reading range and many more settings.

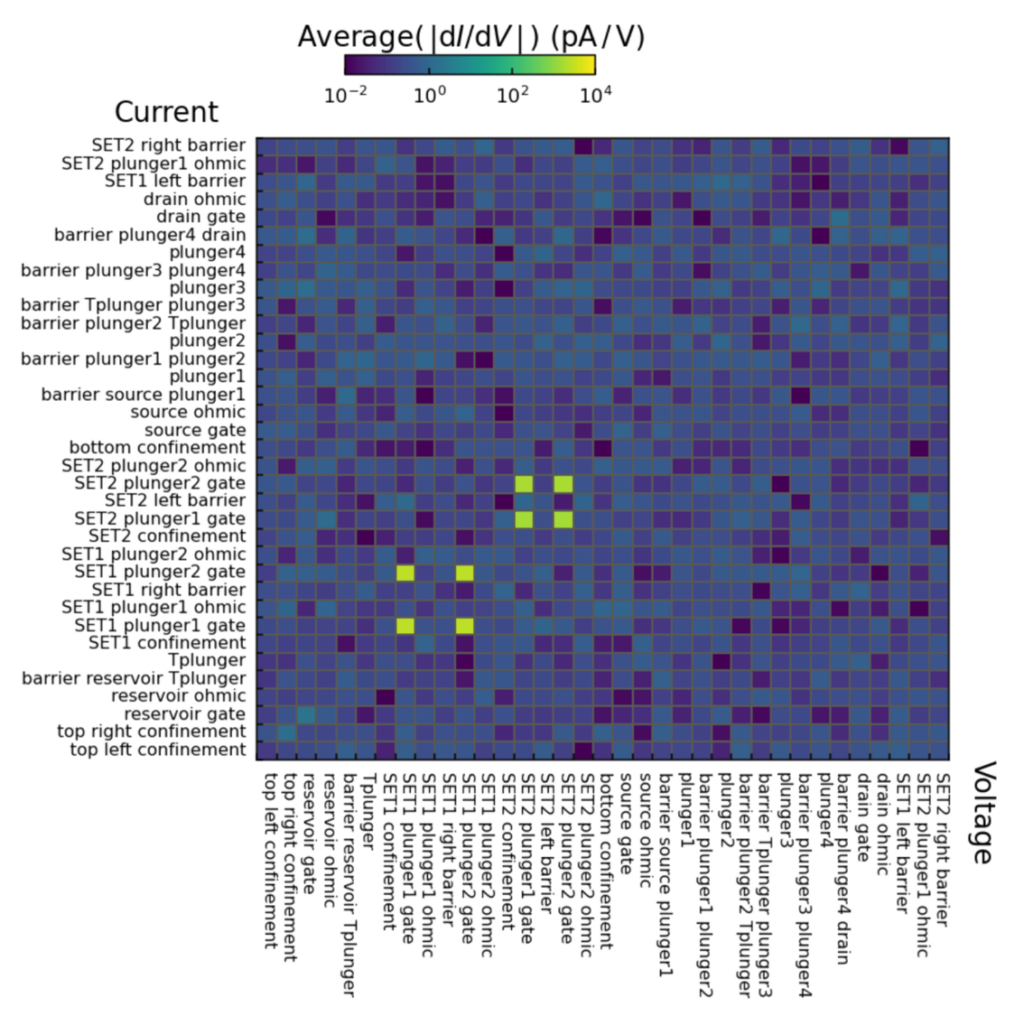
Figure 2: Leakage matrix results obtained with two QDAC units, allowing for fast looping and results within seconds, for a 4-spin qubit QPU. Data courtesy of Sofia Patomäki and Quantum Motions. Additional examples and information are available in [4].

Each channel also features five waveform generators and 1 GB of memory for uploading arbitrary sequences. The QDAC family can read input current from the QPU, enabling the routine of a leakage matrix characterization, available in the QCoDeS repository [3].  

This characterization quickly checks the device’s status by monitoring leakage currents between the quantum dot network electrodes. The number of measurements required scales quadratically with the number of gates, e.g., amounting to 576 measurements for 24 gates.

This can take hours when done manually, but QDAC allows for an automated process which reduces running time to mere minutes. In Figure 2, we show a leakage matrix measured in a few minutes with two synched QDAC for a 4-spin qubit chip.

Once the spin qubit network is cold inside the dilution refrigerator, the first step is to characterize the basic properties of the device, such as gate electrodes status. This can be easily done using Quantum Machines’ QDAC-II, which enables leakage matrix capabilities. QDAC-II and QDAC-II Compact are 24-channel DACs offering ultra-low noise (< 8 nV/√Hz) and high accuracy voltages with 25-bit resolution over a +/- 10V and +/- 2V. Users can independently configure each channel’s output filters, voltage, voltage range, current reading range and many more.  

Once basic tests have been performed, the next steps consist of multiple workflows such as identifying turn-on and pinch-off voltages, forming quantum dots, finding single electron regimes, and optimizing sensor quantum dots. Different tuning steps require different experimental configurations, such as switching between current sensing and reflectometry readout. With the QSwitch, the changes in the experimental setup can be software controlled and become part of the automated tune-up procedure. QSwitch is a fully automated switch matrix, which can directly interface with the QDAC and the dilution refrigerator, as shown in Figure 3.

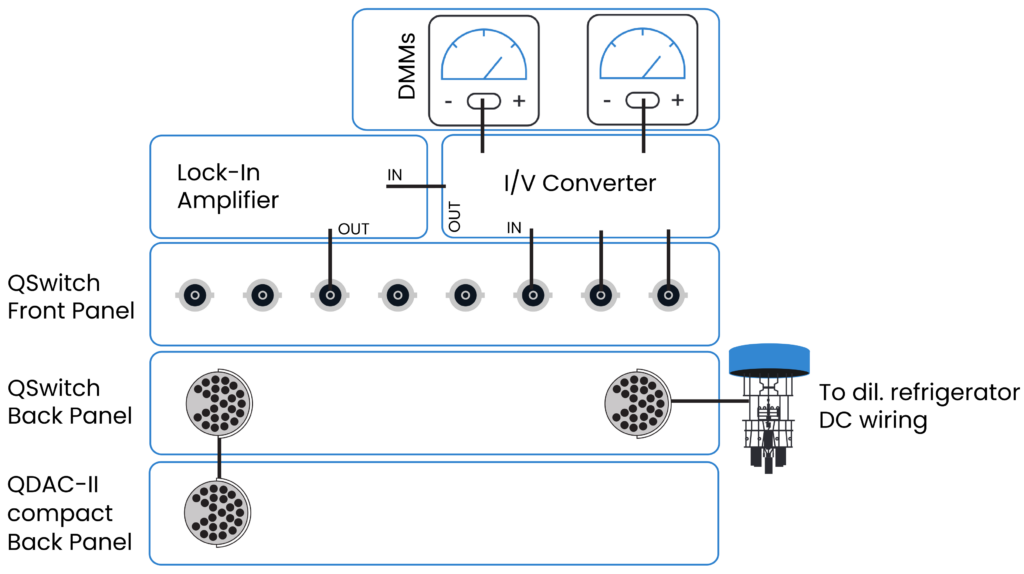
Figure 3: Usage of Qswitch for the DC wiring of a dilution refrigerator.

QSwitch is optimized to maintain the low voltage noise generated by the QDAC while enabling automated operations, thanks to the optimized arrangement of the internal relays. Furthermore, QSwitch is designed to protect the semiconductor device during any operations, relying on the standard “make-before-break” switch procedure as well as default soft grounding of the lines if the setup is suddenly to lose power. Programming of the QSwitch is fully supported on QCoDeS.

Tuning to the single electron regime

The next steps toward the isolation of single electrons in quantum dots concern the depletion of the quantum dots by fine tuning the gate voltages. Performing this task can be quite time-consuming since it requires exploring a parameter space that scales linearly with the number of qubits and can cover a large voltage space. With Quantum Machines’ products, this can be done in two ways.

One: It is possible to use QDACs to scan the parameter space simultaneously measuring the readout current directly with the QDAC making it a simple, all-in-one solution. This acquisition method is limited by the low pass filters of the ADCs, limiting the bandwidth to 1KHz, and the SNR of the direct current measurement.

Two: To access larger bandwidth and enable reflectometry or dispersive readout in the radiofrequency and microwave bands, the signal readout can be orchestrated by the OPX while leveraging its integration with QDAC to provide the lowest-noise control signals through QBoard-II’s cryogenic bias tees. In the next paragraph we will show a specific use case with this type of integration.

More advanced examples as well as information about charge stability diagrams with QDAC can be found in the QM seminars: QDAC-II Compact: Low-Noise 1U DAC and Physics-informed tracking of qubit fluctuations.

In the following example we use the OPX and QDAC to measure a charge stability diagram within milliseconds with just a few lines of QUA code. The OPX enables control, readout and live processing of data in a comprehensive manner. Making use of the QBoard-II integrated bias-tees, signals coming from the OPX and the QDAC can be combined at cryogenic temperatures for each quantum dot control electrode. This enables ultrafast sampling of the charge stability diagrams, speeding up the tune up processes for spin qubit chips. With reference to the setup in Figure 1, we can write the simple QUA code shown below to run a stability diagram.

definition of triggered QDAC actions  
# can be written in Python, QCodes, or any other 
Ch1 = qdac2.channel(1) 
Vg1_list = ch1.dc_list(voltages=voltage_values1, stepped = True) 
Vg1_list.start_on_external(trigger=1) 
Ch2= qdac2.channel(2)
Vg2_list = ch2.dc_list(voltages=voltage_values2, stepped = True)
Vg2_list.start_on_external(trigger=2) 

 
# looped QUA sequence
With for_(n, 0, n < n_avg, n+1):
     With for_(i, 0, i < len(voltage_values1), i+1):
          play(“trigger”, “qdac_trigger1”)
          with for_(j, 0, j < len(voltage_values2), j+1):
               play(“trigger”, “qdac_trigger2”)
               Wait(qdac_settle_time, “readout_element”)
               Measure(“readout”, “readout_element, ..., I, Q) 

In the python code above, we see a few python commands for the QDAC, defined in the QCoDeS driver:

The dc_list() function allows to load a list of up to 60K points to any channels of the QDAC. Each point represents a voltage value that the QDAC can be stepped to. It is possible to iterate between the list points using an internal or external trigger.

The start_on_external() function enables a channel of the QDAC to be ready to receive a trigger event coming from an external source. QDAC-II family has up to 4 external triggers available, and multiple QDAC channels can be configured to be listening to the same trigger input.

While, in the QUA code above we see a few commands for the OPX:

The play() command is used to generate a pulse, generally capable of real-time parameter updates. In this case, however, a simple trigger pulse from the digital markers is generated to step QDAC voltages in a list-mode.

wait() does exactly that, halting program execution for a specified time. In this application we wait for the QDAC to settle to a new voltage before we proceed.

The measure() command, acquires ADC signal and processes it, using various demodulation or integration methods. Here, the measure command is used to acquire data every time we move to a new voltage point.

The result of such protocol is shown in Figure 4.

Figure 4: Charge stability diagram collected in minutes with OPX used to measure and trigger QDAC-II. Data courtesy of Bobby Luo from the University of Cambridge and Tsung-Yeh Yang from the Hitachi Cambridge Laboratory.

The OPX can perform scans changing voltage points in hundreds of nanoseconds, but the voltage range on the device is typically smaller since attenuators are often used on the high-frequency lines inside the dilution refrigerators. The QDAC-II, on the other hand, can produce a larger voltage range due to a wider voltage swing at the device (enabled by the absence of attenuation on the low frequency cabling inside the dilution refrigerator).

Since the update rate on the QDAC-II is as fast as 1 µs, the low pass filter cutoff frequency typically sets an upper bound on the acquisition rate. With more advanced readout techniques, though, the acquisition can be done much faster than a microsecond. In these cases, the QDAC-II & OPX combo allows for more advanced scans where the QDAC-II moves to a new voltage point, and the OPX performs Raster scans (see Figure 5), or more advanced scans around that point, limited only by the measurement SNR. This combined pattern of fast OPX raster and slower QDAC-II scans enables the acquisition of a large but detailed map, with a new level of speed and flexibility. Such considerations become more important as the size of the chip and the parameter space increases. QUA examples for Raster and more advanced scans can be found our GitHub page.

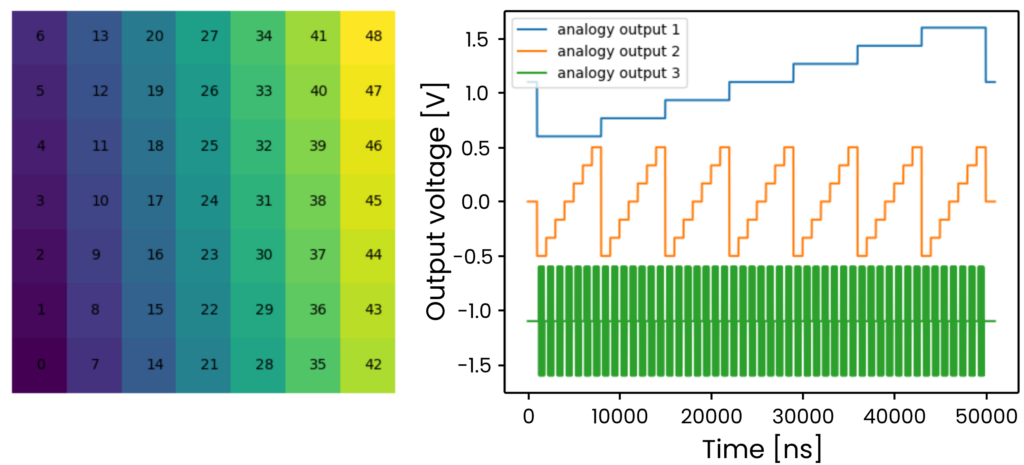
Figure 5: Raster scan done with OPX+. The output voltages have been offset by 1.1V for clarity. Any type of scan can be easily implemented on OPX. Read more on our GitHub page.

Another example of flexible programming and powerful real-time computation is the ability to easily perform useful routines such as embedded calibrations, using the OPX. This is crucial for semiconductor materials that suffer from voltage noise effects due to material imperfections, inducing slow drift of the biasing voltages as well as sudden charge jumps. An advanced embedded calibration routine for quantum dots, used here as an example, is implementing PID feedback loop to stabilize the charge sensor used for readout. Even more advanced examples of feedback and stabilization have been demonstrated with the OPX platform by the Diraq’s team [5].

Using the standard simplified configuration shown in Figure 6, the electrode that controls the charge sensor bias is connected to the OPX output while the signal generated by this sensor is fed to the to the OPX input. The OPX real-time calculation capabilities are used to calculate the error signal produced by the deviation from the optimal readout point and apply a correction evaluated using PID feedback equations. The code snippet below shows how the routine is implemented using QUA. Using this code, PID loops can be implemented with an update rate of roughly 350 ns per shot.

With infinite_loop():
     Play(“correct”*amp(A), “Sensor_gate”)
     Measure(“readout”, “Sensor_readout”, None, integration.full(“const”, point, “out2))
 
Assign(error, (point-set_point) <<1) 
Assign(accum, (1-alpha) *accum + alpha*error) 
Assign(gradient, error – prev_error) 
Assign(A, A + Kp*error + Ki*accum + Kd*gradient)

Within the infinite_loop() flow which runs indefinitely, the measurement outcome of the charge sensor is stored in the real-time variable point. The proportional (error), integral (accum) and derivative (gradient) error values are calculated (note that in QUA assign() takes the role of the equal sign). In the last line the updated value of the amplitude scaling factor is composed using the predefined PID parameters. In the next iteration of this loop, the new amplitude is used to correct the biasing point of the charge sensor using *amp().

Figure 6: Sketch of the OPX+ control of a charge sensor with PID stabilization over voltages. Examples of how PID loops are used for stabilization of spin qubit systems can be found in [4].

Expediting tune-up

One of the main challenges in tuning up quantum dots is the large parameter space that needs to be explored. Beside optimizing the plunger electrodes to shape properly the quantum dots, it is also crucial to tune the tunnel coupling to the right value to observe Pauli spin blockade as well as getting the right tunnel rates to perform Elzerman readout. To speed up quantum dot network, a common technique used is “video mode”. By relying on reflectometry readout, with bandwidth in the order of tens of MHz, charge stability diagrams can be streamed from the OPX to the client PC reaching a refresh rate up to 20 fps (depending on the readout SNR and the chosen resolution).

Quantum Machines has developed a modular video mode architecture which relies on a modular backend server to harness the full power of the QUA language. Using video mode parameters can dynamically tuned, speeding up spin qubit experiments. Two main classes define the QUA program that is being uploaded to the OPX to optimize video mode acquisition, the ScanModes() and the InnerLoopAction(). The ScanModes() class is responsible for how the 2D charge stability diagram is explored, depending on the setup configuration. The InnerLoopAction() includes the QUA code used once the main 2D charge stability diagram parameters have been set. The easiest option is to perform a measure() command, but more advanced sequences, as Pauli Spin Blockade protocols, can be seamlessly implemented.

Eventually the VideoMode() class handles the streaming to the frontend where the data can be visualized on a web-based interface. Specific parameters, such as voltage resolution and span as well as averaging can be dynamically modified as shown below. The video mode class, together with the standalone GUI for gate voltage settings, allows for a truly interactive tune-up experience, as we show in Figure 7.

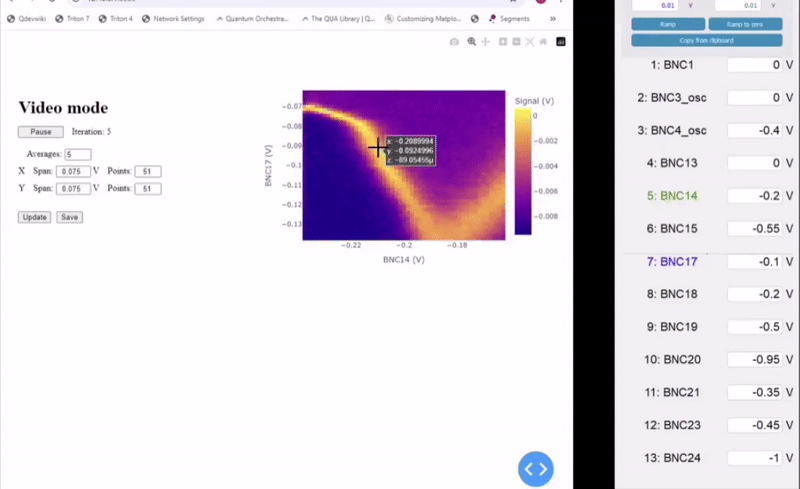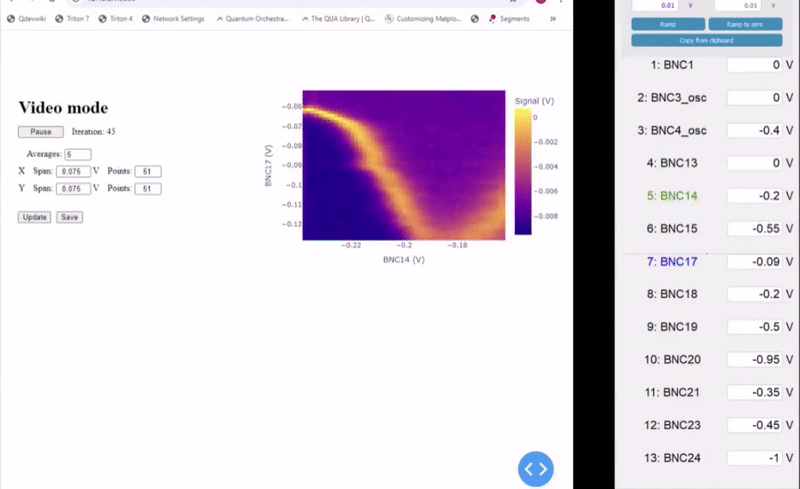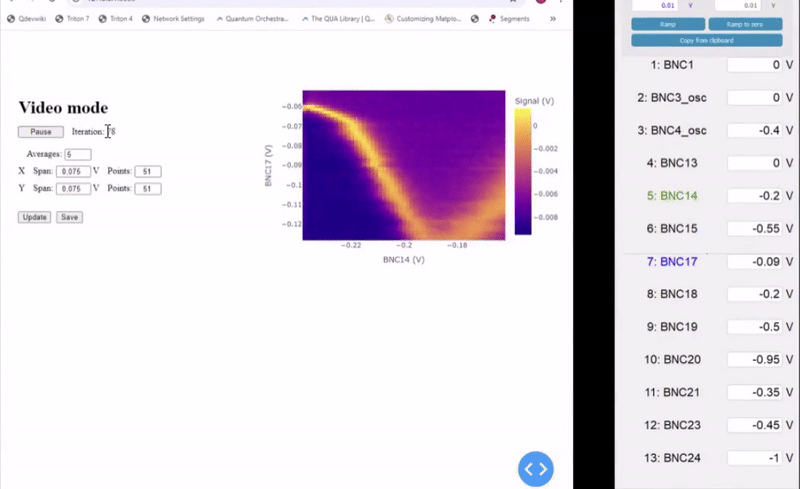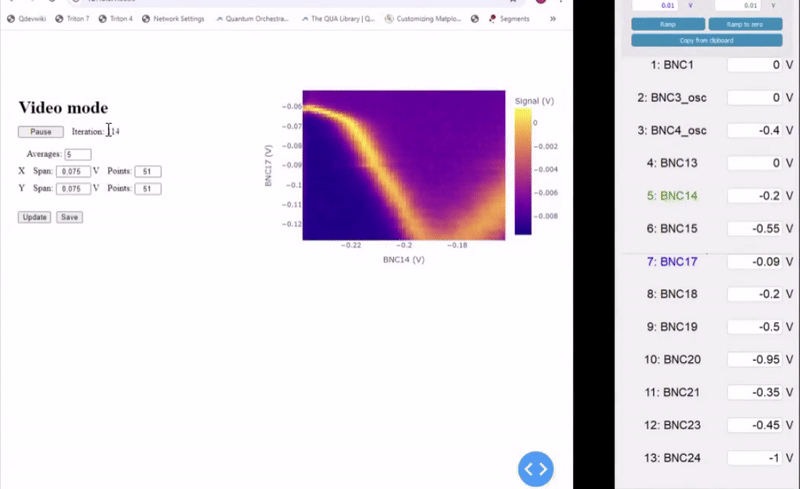
Figure 7: Sped-up animation showing Video Mode in action, together with the live GUI for gate voltage control of the QDAC, allowing for a fully interactive experience.

Although the Quantum Machines control suite makes it easy to measure stability diagrams, it might not always be easy to gather a large variety of data from different devices, required to for instance train automated tuning algorithms on. For this purpose, Quantum Machines can recommend using a realistic quantum dot array stability diagram simulator, such as QDarts , developed by research teams from the Universities of Copenhagen and Leiden, with the support of Quantum Machines (you will be able to read more on QDarts in our blog soon). Other stability diagram simulators to choose from are QArray, developed at the University of Oxford, and QDSim, developed at the Delft University of Technology. These software packages can be used to fit the data and extract parameters of interest or quickly generate numerous charge stability diagram maps with realistic device parameters to train  an AI-powered tuning algorithms, before applying them in your experiments. 

Spin qubit characterization starter kit

Once quantum dots have been tuned-up, thermalized, populated and stabilized, the quantum dot network can now be operated as a quantum processor unit (QPU). Whether your qubits are Loss-DiVincenzo with their synthetic spin orbit field, Spin-Triplet qubits or Exchange-only with their all-electrical control, the OPX1000 and QDAC-II offer the ideal control suite for performing quantum gates, readout and analog feedback from a single unified brain. On the readout side, the advanced capabilities of the OPX architecture can seamlessly perform spin-to-charge conversion whether based on Pauli exclusion principle or Elzerman readout. Once the signal has been acquired, the OPX can then performs live analysis for minimal delays with fast feedback and feedforward, in order to optimize the next iteration of quantum error correction cycle. Let’s now have a look at operations on qubits, from characterization examples to some advanced applications.

Here is an example of T1 measurements for spin qubit implemented for Elzerman style readout. We control the OPX operation by writing instructions in QUA, OPX controllers’ open-source pulse-level language. The QUA code gets uploaded in less than 1 second, and then the sequence runs solely on the PPU, rendering loops and sequences much faster, with no compilation time or memory loading overhead, even for arbitrarily long sequences. For a single qubit, here is how we can code such an experiment in QUA, and we show in Figure 8 a sketch of the resulting measurement and the sequence used in the code.

With program() as Elzerman readout: 
     with for_(n, 0, n < n_avg, n + 1):        #Averaging loop 
         with for_(*from_array(tau, taus)):    #Delay loop 
              play(“electron_injection”,”Plunger_Qubit”)
              align()
              play(“readout_point”,”Plunger_Qubit”) 
              wait(tau, "SET_Readout", "Plunger_Qubit") 
              measure("readout", "SET_Readout", None, demod.full("cos",I), demod.full("sin",Q))
              ramp_to_zero(“Plunger_Qubit”)
              save(I, I_st) 
              save(Q, Q_st) 
     with stream_processing(): 
          I_st.buffer(len(tau)).average().save("I") 
          Q_st.buffer(len(tau)).average().save("Q")  

Figure 8: Schematics of the results for (a) a T1 measurement and (b) the sequence used to obtain it.

We operate in two for() loops, for averaging and sweeping. This is easily extended to multi-qubit characterization with an additional loop. We have already seen how the play(), wait(), and measure() operate. Note that the wait command does not have an upper limit, as well as the “Readout_Point” pulse, meaning that with the OPX architecture it is straightforward to measure T1 which are seconds long, without affecting the upload time. When measuring long T1 it is also needed to compensate the effect of the bias-tee, by introducing high pass correction filtering. This can be easily implemented in the definition of the pulse element by using the filter() keyword and it is seamlessly implemented using the native FIR and IIR filters. Lastly, the stream_ processing() allows to save, fetch and process data on the 16-core co-processor tightly integrated with the PPU. The co-processor operates in parallel with the PPU to enable fast data streaming (performing heavier processing and avoid clogging the lab network) while maintaining short program run-times.

Another way to implement the measurement of T1, is to use sliced demodulation, implementing the command demod.slice() configuration within the measure() command, as implemented in the QUA library GitHub.

T1 measurements using the previous code can be straightforwardly extended to Pauli spin blockade. In the following code we are now going to introduce the VoltageGateSequence() class which we have developed in order to help the spin qubit users to easily implement voltage sequence pulses based on charge stability diagrams. The experiment is implemented with reference to Figure 9, where we show the pulse coordinates and sketch the sequence. We will skip the stream processing in the codes below, but it is always available.

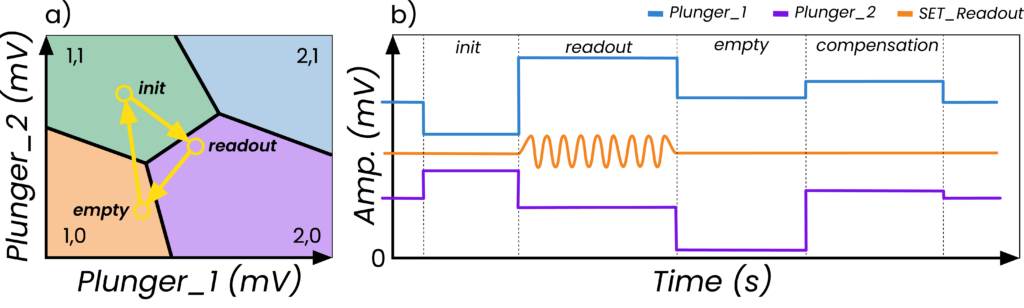
Figure 9: T1 measurement extended to Pauli spin blockade. (a) 2D stability diagram with pulse sequence steps and (b) Pulse sequence used to perform PSB measurement.

seq = OPX_virtual_gate_sequence(config, ["Plunger_1", "Plunger_2"]) 
seq.add_points("empty", level_empty, duration_empty) 
seq.add_points("init", level_init, duration_init) 
seq.add_points("readout", level_readout, duration_readout) 

with program() as PSB_search_prog: 
    with for_(i, 0, i < Plunger_1_pts + 1, i + 1): 
        with for_(j, 0, j < Plunger_2_pts, j + 1): 
            #DC_gates update 
            ... 
            # Play PSB triangle sequence 
            seq.add_step(voltage_point_name="empty") 
            seq.add_step(voltage_point_name="init") 
            seq.add_step(voltage_point_name="readout")
            seq.add_compensation_pulse(duration=duration_compensation_pulse) 
            # Measure the dot right after the qubit manipulation 
            wait((duration_init + duration_empty) * u.ns, "SET_readout") 
            measure("readout", "SET_Readout", None, demod.full("cos",I), demod.full("sin",Q)) 
            seq.ramp_to_zero()

In the code above the Plunger_1_pts and Plunger_2_pts represent the DC biasing points of the charge stability map that are going to be explored. We have also extended the implementation of the wait(), where now only the element “SET Readout” is waiting in order to align the measurement command with the “readout” segment of the pulse sequence. The VoltageGateSequence() class, containing useful functions like add_step(), allows seamlessly building complex gate pulsing sequences. It is also straightforward to convert a an add_step() element from a baseband pulse to a ramp sequence by introducing the keyword duration within add_step(). The class is already optimized to ensure a zero DC offset coming from the voltage pulse sequence, implementing the add_compensation_pulse() command. A full example for PSB readout can be found in the QUA libraries.

Furthermore, when performing pulse sequence using the VoltageGateSequence() class, QUA allows to implement dynamical cross talk matrix correction by associating the keyword crosstalk to a specific element in the configuration file. This crosstalk matrix allows to correct for the finite cross talk existing between adjacent qubits, ensuring that the pulse sequence implemented will not affect the configuration of nearby quits in the QPU.

As T1 has been identified for all the qubits in the QPU, the next step concerns the implementation of spectroscopy experiments aimed at discovering the operational frequency of the qubits. In the following example we will consider the case for a linear array of Loss-DiVincenzo qubits, as outlined in the geometry in Figure 1. For qubit spectroscopy we must repeatedly drive and measure each qubit, while sweeping frequency and averaging the results. Here is an example QUA code:

With program() as spectroscopy: 
     with for_(n, 0, n < n_avg, n + 1): 
          with for_(*from_array(f, frequencies)): 
          # Update the frequency of the Drive_Line element 
          update_frequency("Drive_Line", f) 
          seq.add_step(voltage_point_name="init") 
          seq.add_step(voltage_point_name="drive") 
          seq.add_step(voltage_point_name="readout")
          seq.add_compensation_pulse(duration=duration_compensation_pulse) 
          #play qubit_drive for spectroscopy 
          wait((duration_init)*u.ns, “Drive_Line”) 
          play(“qubit_drive”,”Drive_Line”, chirp=chirp_rate , 'Hz/nsec')) 
          # Measure the dot right after the qubit manipulation 
          wait((duration_init + duration_empty) * u.ns, "SET_Readout") 
          measure("readout", "SET_Readout", None,    demod.full("cos",I), demod.full("sin",Q)) 
          seq.ramp_to_zero()

 

Where the update_frequency() command parametrically updates the frequency of the drive tone in the QUA program. In order to speed up the identification of the resonance frequency of the qubits, given its narrow bandwidth in frequency domain, we have introduced the chirp keyword. By selecting the correct chirp_rate, resonant features can be quickly found.

Following spectroscopy, there are many other characterization protocols that can help further the understanding of the qubit, to gather information about coherence times and more. Other experiments, like the Rabi sequence shown in Figure 10, involve a more complicated sequence of pulses and dynamic waits. This is written in QUA as simply as pseudocode.

 

Figure 10: Schematics of the results for (a) a 1D Rabi measurement and (b) the pulse sequence used to obtain the measurement.

 

This sequence can easily become a 2D Rabi-Chevron map with one additional for() loop for the frequency of the drive. In the code example below, we show two sweeping parameters, frequency and pulse duration, which are programmed easily in QUA, and performed at the lowest level of the hardware by the OPX, offering unmatched speed of execution.

With program() as Rabi-Chevron: 
      with for_(n,0,n<Navg,n+1): 
           with for_(t,t_ini,t<t_final,t): 
                with for_(f,f_ini,f<f_final,f+df): 
                     # Update the frequency of the Drive_Line element 
                     update_frequency("Drive_Line", f) 
                     seq.add_step(voltage_point_name="init") 
                     seq.add_step(voltage_point_name="drive") 
                     seq.add_step(voltage_point_name="readout")
                     seq.add_compensation_pulse(duration=duration_compensation_pulse) 
                     #play Rabi_pulse 
                     wait((duration_init)*u.ns, “Drive_Line”) 
                     play(“Rabi_pulse”,”Drive_Line”,duration=t) 
                     # Measure the dot right after the qubit manipulation 
                     wait((duration_init + duration_empty) * u.ns, "SET_readout") 
                     measure("readout", "SET_readout", None,    demod.full("cos",I), demod.full("sin",Q 
                     seq.ramp_to_zero()

Thanks to the unique Pulse Processing Unit (PPU) architecture, there is no waveform being uploaded between runs. Waits and plays are evaluated as instructions, and waveforms are stretched and modified in real-time. The averaging is now performed in the outer loop, enabling acquisition of a full map before averaging, heavily reducing the impact of slow drifts in the system. These features allowed the Rabi-Chevron measurement in Figure 11, to be taken in just 4 minutes by the team of Prof. Andrew Dzurak at UNSW.

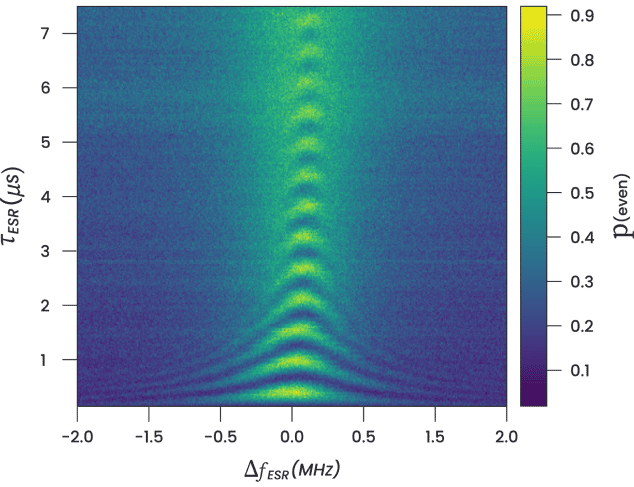
Figure 11: Rabi-Chevron measurement measured with the OPX+. The probability of an even spin state is plotted against the ESR pulse duration and frequency. This measurement was performed on a grid of 300X400, averaged 100 times, and took approximately 4 minutes to run. Data on Si-MOS quantum dot qubits courtesy of Will Gilbert, from the group of Prof. Andrew Dzurak, UNSW-Sydney.

Advanced characterization and beyond

Randomized benchmarking (RB) is one of the go-to experiments to show the quality of operation of a QPU, measuring the average error rate of a quantum gate. RB requires us to iterate a random sequence of randomly sampled gates. Due to its intrinsic random nature and its loops, RB-like protocols heavily benefit from a controller able to generate and randomize pulses (even in real-time if needed), directly on the lowest level of the control hardware and according to a specified logic. This alleviates the challenges associated with play-from-memory controllers, which tend to introduce significantly more overhead.  

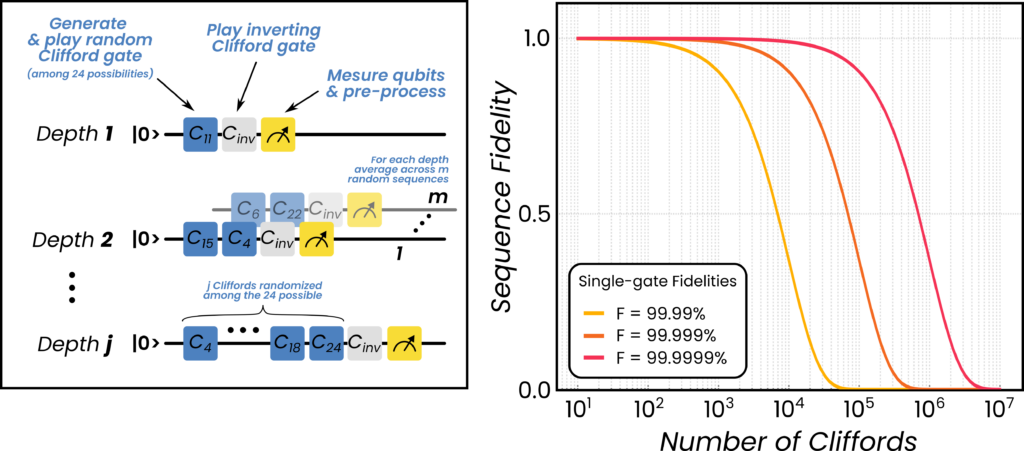
Figure 12: (a) Randomized benchmarking (RB) protocol sketch and (b) simulated state probability trends (sequence fidelity) for systems with different single-gate fidelities, showing the RB depth necessary to achieve fidelities of 4,5 and 6 nines. The Pulse Processing Unit (PPU) of the OPX controller allows for arbitrarily-long RB sequences, enabling measurements of ever-increasing fidelities.

A sketch of the RB process and the simulated fidelity is shown in Figure 12. From this simulation we see that, with high-fidelity gates, we require controllers able to handle increasingly long randomized sequences. The PPU allows users to randomize and generate the sequences at the lowest level of the hardware. With its instructions-based loops and inherently low latencies, the OPX allows for RB with arbitrary depth, out of the box. 

Let’ s take a look at an example of RB code written in QUA. The code is composed of three building blocks, two of which are macros (step 1 and 2), that are integrated and executed as part of the RB protocol (step 3). 

We start by building the components of the protocol in comfortable macros. In fact, macros are a very useful tool available in QUA, as they allow to build resources and routines specific to your setup that can be reused simply and effectively. 

1. Generation of random Clifford sequences and calculation of their inverses based on the rand() command.

2. Real-Time Gate Execution utilizing QUA switch logic based on the switch_() command.

3. QUA RB Protocol: combines step 1 & 2 into a streamlined, real-time quantum classical workflow with efficient data management in and out of the PPU.

First things first, we need to be able to generate a random sequence, therefore we construct the macro generate_sequence() in step 1 (the following code is stripped down to highlight the main features required to run the program. The full example can be found in our github): 

inv_gates = [int(np.where(c1_table[i, :] == 0)[0][0]) for i in range(24)] 

def generate_sequence(): 
    rand = Random(seed=seed) 
    assign(current_state, 0) 
    with for_(i, 0, i < max_circuit_depth, i + 1): 
        assign(step, rand.rand_int(24)) 
        assign(current_state, cayley[current_state * 24 + step]) 
        assign(sequence[i], step) 
        assign(inv_gate[i], inv_list[current_state]) 
    return sequence, inv_gate

Using the OPX platform it is possible to randomize the Clifford sequence required at every step of the RB protocol by simply calling the rand() QUA function. This function makes use of the 32-bits random number generator inside the OPX. The macro will be useful to generate arbitrarily long random sequences later, while also tracking their inverse. 

Next, we should also make a macro to apply the Clifford gates (step 2). Here we can use the switch case available in QUA to generate all the different cases. We won’t type all 24 of them here, but the concept should be clear:

def play_sequence(sequence_list, depth): 
    with for_(i, 0, i <= depth, i + 1): 
        with switch_(sequence_list[i]): 
            with case_(0): 
                wait(x180_len // 4, "qubit") 
            with case_(1): 
                play("x180", "qubit") 
#...more cases here 
            with case_(23): 
                play("-x90", "qubit") 
                play("y90", "qubit") 
                play("-x90", "qubit") 

We see here how easy it is to construct complicated branching using the QUA switch_() logic, a flexible and efficient way to implement advanced real-time control flow based on the value of a variable. The switch case logic is performed in real time, so the variable could even be the result of a measurement. Here we use switch to run over all 24 cases that make up a complete Clifford group. 

Lastly, we need to calculate the time it takes to run the sequences in each case. This is necessary to correctly calculate correction, to be able to correctly associate durations when calculating the compensation pulse sent at the end of each sequence. The code is very similar to play_sequence(), but assigns durations instead of playing. 

def generate_sequence_time(sequence_list, depth): 
    Assign(duration, 0) #ensures duration is reset to 0 for every depth 
    with for_(j, 0, j <= depth, i + 1): 
        with switch_(sequence_list[i]): 
            with case_(0): 
                assign(duration, duration + x180_len) 
            with case_(1): 
                assign(duration, duration + x180_len)  
#...more cases here 
            with case_(23): 
                assign(duration, duration + minus_x90_len + y90_len + minus_x90_len) 

The two macros are added to the main program to form the complete RB code in QUA: 

with program() as rb: 
    #...various declarations  

    with for_(m, 0, m < num_of_sequences, m + 1):  #QUA for_ loop over the random sequences 
        sequence_list, inv_gate_list = generate_sequence()   
        assign(depth_target, 1)  #Initialize the current depth to 1 
        with for_(depth, 1, depth <= max_circuit_depth, depth + 1): 
            assign(saved_gate, sequence_list[depth]) 
            assign(sequence_list[depth], inv_gate_list[depth - 1]) 
            with if_(depth == depth_target):  #only play target depth 

                assign(sequence_time, generate_sequence_time(sequence_list, depth)) 
                seq.add_step( voltage_point_name="initialization") 
                seq.add_step( voltage_point_name="idle", duration=sequence_time + RB_delay) 
                seq.add_step( voltage_point_name="readout", duration=readout_len) 
                seq.add_compensation_pulse( duration=duration_compensation_pulse) 

                wait((duration_init * u.ns), "qubit") 
                play_sequence(sequence_list, depth) #play sequence of Cliffords 
                wait( duration_init * u.ns) + (sequence_time >> 2) + (RB_delay >> 2), "tank_circuit”) 

                I, Q, I_st, Q_st = RF_reflectometry_macro(I=I, Q=Q) 

                if state_discrimination: 
                    save(state, state_st) 
                else: 
                    save(I, I_st) 
                    save(Q, Q_st) 
                seq.ramp_to_zero() 
                assign(depth_target, depth_target + delta_clifford) 
            assign(sequence_list[depth], saved_gate) 

The code runs over several nested loops. The first loop runs over the QUA variable m, and creates the random sequence of Cliffords for each depth. This step is done using the generate_sequence() macro. In this loop we also define the final recovery gate. The second loop runs on depth, covering over all depths of the RB protocol.  The protocol starts by setting the baseband pulse sequence (those have been defined in the declaration, similarly to the examples in the previous chapters), then playing the randomized sequence, and finally reading out, e.g. via RF reflectometry. Check the full example code in our Github repo for Spin Qubits. 

The last part of the code saves the data into streams using the stream_processing() as we introduced in the sections above. In this case, we can use it to perform live averaging, allowing the retrieval of pre-processed data and avoiding clogging the lab network. Such calculation would be done using the map(FUNCTIONS.average()) feature within the same QUA program (not shown here). The map() function allows advanced pre-processing to be done on a subsection of the data buffers while the experiment is still running.  

Given the modularity of the code introduced above, it is possible to easily extend the protocol to interleaved RB (iRB), which is useful to extract fidelities for the individual gate operations. The only part that would have to change is the definition of the macro used to generate the RB sequence as follow: 

def generate_sequence(interleaved_gate_index): 

    #...various declarations  

    rand = Random(seed=seed) 
    assign(current_state, 0) 

    with for_(i, 0, i < 2 * max_circuit_depth, i + 2): 
        assign(step, rand.rand_int(24)) 
        assign(current_state, cayley[current_state * 24 + step]) 
        assign(sequence[i], step) 
        assign(inv_gate[i], inv_list[current_state]) 

        # interleaved gate 
        assign(step, interleaved_gate_index) 
        assign(current_state, cayley[current_state * 24 + step]) 
        assign(sequence[i + 1], step) 
        assign(inv_gate[i + 1], inv_list[current_state]) 
    return sequence, inv_gate 

Suppressing qubit dephasing via real-time Hamiltonian estimation

The OPX real-time capabilities can be harnessed for a variety of feedback operations. A particularly compelling example of this is implementing Bayesian estimation techniques to estimate fluctuating parameters in the Hamiltonian. This is particularly beneficial for metrology or, in this case, to extend the coherence time of qubits. The required rate of feedback depends on the frequency with which the environment parameter is fluctuating. Or the other way around, the faster the feedback can be applied, the higher the frequency of noise that can be mitigated by the OPX. In the example below, the Bayesian estimation is taken to the extreme limit, in which one of the qubit control axes is solely governed by the fluctuating environment (flip-flopping nuclear spins).

We will now consider a double quantum dot system populated with two electrons. Such a system encodes a S-T0 qubit in GaAs/AlGaAs as shown in [6] and [7]. The two axes of controls of the qubit are the exchange interaction J between the two electrons as well as the gradient of magnetic field ΔB between the two quantum dots. This gradient is due to the non-zero spin isotopes of Ga, Al and As which form the substrate, and is also known as Overhauser field. It slowly fluctuates over milliseconds long time scales.

Such timescales are much slower compared to the typical S-T0 qubit operation times. T2* is in the order of tens of nanoseconds when averaging over seconds of data, exactly because of the averaging over the magnetic fluctuations. Correcting for those fluctuations extends T2* substantially. As the drive ΔB fluctuates, so does the time required to implement a Z gate. However, if it could be possible to know the exact magnetic field before performing any qubit operation, coherences could be extended much longer and universal axis control can be achieved in this system. This has been achieved in both [6] and [7] by implementing real time Bayesian estimation of the Overhauser magnetic field gradient, which, when interleaved with qubit control sequences, has extended qubit rotations by ten times. In [7] the experiment was performed using the real-time capabilities of the OPX connected with a QDAC-II.

Bayesian estimation uses a prior postulate by which all magnetic field gradient values in some ranges are equally probable and uses Bayes theorem to update the (posterior) distribution repeatedly. The final distribution’s most probable field is assumed to be the external field for the experiment’s duration.

To perform Bayesian estimation, first, we must perform a single-shot state evaluation. This is done in the first row of the snippet below. The state is measured by measuring the reflection of an RF signal from a single electron transistor (SET) near the double-dot. The reflected signal is demodulated, and the demodulated value is saved to a variable. We accomplish all this with just a single statement.

The following expression then needs to be repeatedly evaluated (in real-time) for each possible value of the magnetic field:

𝑃(𝑚𝑘|Δ𝐵𝑧)=1/2[1+𝑟𝑘(𝛼+𝛽𝑐𝑜𝑠(2𝜋Δ𝐵𝑧𝑡𝑘)] 

This is done in the first for() loop. Note the usage of casting and trigonometric functions which are efficiently implemented on the PPU. The second for() loop is a normalization of the resulting probability distribution.

Measure("measure", "RF-QPC", None, demod.full("integQ1", I) 
assign(state[k - 1], I > 0) 
save(state[k - 1], satet_str) 
assign(rk, Cast.to_fixed(state[k - 1]) - 0.5) 
with for_(fB, fB_min, fB < fB_max, fB + dfB): 
     assign(C, Math.cos2pi(Cast.mul_fixed_by_int(fB, t_samp * k))) 
     assign(Pf[ind1], (0.5 + rk * (alpha + beta * C)) * Pf[ind1]) 
     assign(ind1, ind1 +1) 
     assign(norm, 1 / Math.sum(Pf)) 
     with for_(ind, 0, ind1 <Pf.length(), ind1 +1):  
         assign(Pf[ind], Pf[ind] * norm)  

The assign() is used to update the value of a QUA variable, which lives live on the OPX and it is used in the full Bayesian estimation cycle to perform real analog feedback on this system. This section of code, showcases also the extended Math() library which is available within QUA and its functions can be directly accessed to perform timed mathematical operations, such as sum() and cos2pi(), to minimize latencies when performing feedback operations.

We hope this dive into examples for spin qubits was interesting. There is so much more to dive in, different qubit types with different requirements and different protocols with details and intricacies. And we am sure now you have more questions than before starting to read! So, it is a good time to contact us for a virtual demo, where you can ask us live questions on how to perform the most advanced sequences you have in mind, or simply to wonder how a setup for controlling your qubits would look like.

Don’t wait any further. Let’s chat!

References 

[1] Van der Heijden, Joost. Electron Thermometry. arXiv preprint arXiv:2403.16305 (2024). 

[2] Hansen, Elias Roos, Ferdinand Kuemmeth, and Joost van der Heijden. Low-temperature benchmarking of qubit control wires by primary electron thermometry. arXiv preprint arXiv:2403.17720 (2024). 

[3] J. H. Nielsen, Qcodes/qcodes: Qcodes 0.43.0 (2024) 

[4] Patomäki, S. M., et al. Elongated quantum dot as a distributed charge sensor.  Physical Review Applied 21.5 (2024): 054042. 

[5] Huang, Jonathan Y., et al. High-fidelity spin qubit operation and algorithmic initialization above 1 K.  Nature 627.8005 (2024): 772-777. 

[6] Shulman, M. D. et al, Suppressing qubit dephasing using real-time Hamiltonian estimation, Nature Comm., 5, 1 (2014). 

[7] Berritta, F. et al., Real-time two-axis control of a spin qubit, Nature Comm., 15, 1676 (2024).